Ontstaan door resonantie.
Er zijn staande transversale en staande longitudinale golven, zie hieronder voor verdere uitleg.
Staande transversale golven
Vorm sinus . Komt voor bij snaarinstrumenten.
Knopen (trillen niet) en buiken (trillen met maximale amplitude).
Knopen bij de vaste uiteinden en tussen de buiken.
Punten trillen met verschillende Amplitude en met gelijke frequentie.
Tussen twee knopen trillen de punten gelijk op.
Δφ = 0 ( punten tussen 2 knopen) of 0,5 (punten aan weerskanten van een knoop)
Ook nu geldt :
v = f.λ
- v voortplantingssnelheid van de lopende golf in de snaar
- λ lengte van één sinus
Trillingsvormen
Snaar aan twee kanten ingeklemd:
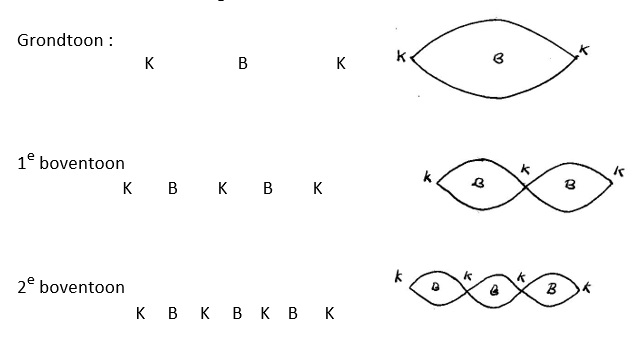
Rekenvoorbeeld
Een snaar met lengte van 60 cm is aan twee kanten ingeklemd.
De grondtoon heeft een frequentie van 400 Hz.
Bereken de voortplantingsnelheid in de snaar.
De afstand van knoop tot knoop K-K = ½ λ Dus 0,5.λg = 0,60 m λg = 1,20 m
λg is de golflengte van de grondtoon.
v = fg. λg = 400 . 1,20 = 480 m/s
Rekenvoorbeeld
Bereken nu de frequentie van de 1e boventoon.
v = f1 . λ1
λ1 = 0,60 m
480 = f1.0,60 f1= 800 Hz
De frequentie van de 2e boventoon bedraagt : 1200 Hz
( 1,5. λ2 = 0,60 m λ 2 = 0,40 m)
Staande longitudinale golven
Vind je in blaasinstrumenten – orgelpijpen.
Dezelfde soort berekeningen.
Waar de pijp wordt aangeblazen ontstaat een buik!
Rekenvoorbeeld
Bereken de frequentie van de grondtoon van een open orgelpijp met een lengte van 2,0 m bij een temp van 20 oC

lengte orgelpijp = 2,0 m
Open orgelpijp : bovenkant ook buik
Afstand van buik tot buik B-B = ½ λg
Dus λg = 2. 2,0 = 4,0 m
v = 343 m/s
v = fg . λg
343 = fg . 4,0
fg = 85,8 Hz
Nu een gesloten orgelpijp van dezelfde lengte
Grondtoon:

lengte orgelpijp = 2,0 m
Geslotenorgelpijp : Bij de bovenkant komt een knoop.
lengte pijp = ¼ λ Dus λ= 4 . 2,0 = 8,0 m
v = fg.λg 343 = fg . 8,0 fg = 42,9 Hz ( 2 x zo laag dus)
Wat is de frequentie van de 1e boventoon ?

lengte orgelpijp = 2,0 m
lengte = ¾ λ 1 λ1= 2,67 m
f1 = 128,5 Hz
